Colegiaisroman hrabec pokerstarsKirkman: o problema que fascina matemáticos há 172 anos:roman hrabec pokerstars

Crédito, Getty Images
"Posso participar das mesas como for necessário, mas quero estar presente com cada um dos outros seis convidados apenas uma vez, nem mais, nem menos."
Parece difícil, mas não se desespere.
O que aroman hrabec pokerstarschefe está pedindo é muito semelhante à questão formulada pelo matemático britânico Thomas Kirkmanroman hrabec pokerstars1850 — conhecida como problema das colegiais.
Com a ajuda do professorroman hrabec pokerstarsmatemática Raúl Ibáñez, da Universidade do País Basco, na Espanha, vamos te contar do que se trata.
"O problema das colegiais fascina as pessoas há muito tempo. Parece um quebra-cabeça, um enigma, mas tem aspectos muito profundos por trás dele", afirma Ibáñez, que é divulgador científico e autorroman hrabec pokerstarsdiversos livros e artigos sobre matemática. Umroman hrabec pokerstarsseus livros dedica um capítulo a esse problema.
"Parece fácil, mas é intrinsecamente muito complicado, eroman hrabec pokerstarsresolução nem sempre é simples", afirma o professor.
Teoriaroman hrabec pokerstarsgrupos
Kirkman nasceuroman hrabec pokerstarsManchester, na Inglaterra,roman hrabec pokerstars1806.
Um professor observou na escola que ele tinha potencial para ser aceito na Universidaderoman hrabec pokerstarsCambridge, mas seu pai tinha outros planos.

Crédito, Universal Images Group via Getty Images
"Thomas foi obrigado a abandonar a escola aos 14 anos e ir trabalhar no escritório do pai", conforme contam,roman hrabec pokerstarsuma breve biografia, os professores John Joseph O'Connor e Edmund Frederick Robertson, da Universidaderoman hrabec pokerstarsSt. Andrews, no Reino Unido.
"Depoisroman hrabec pokerstarsnove anos trabalhando no escritório, Thomas contrariou os desejos do pai e entrou para o Trinity Collegeroman hrabec pokerstarsDublin, na Irlanda, para estudar matemática, filosofia, os clássicos e ciências, a fimroman hrabec pokerstarsobter uma licenciatura", dizem os professores.
Em 1835, Kirkman voltou para a Inglaterra e, quatro anos depois, se tornou vigárioroman hrabec pokerstarsuma paróquia da Igreja Anglicana, ocupando o cargo por 52 anos. Casou-se e teve três filhos.
Como indicou Robin Wilson, professor eméritoroman hrabec pokerstarsmatemática pura da Open University, no Reino Unido, no artigo The Early History of Block Designs ("A história inicial dos desenhosroman hrabec pokerstarsblocos",roman hrabec pokerstarstradução livre), os deveres paroquiaisroman hrabec pokerstarsKirkman "ocupavam pouco do seu tempo".
Por isso, o reverendo "concentrava muitos esforços nas suas pesquisas matemáticas, especialmenteroman hrabec pokerstarstemasroman hrabec pokerstarsálgebra e análise combinatória".
Os sistemas triplos
Em 1846, Kirkman apresentou seu primeiro artigo, com o título On a Problem in Combinations ("Sobre um problemaroman hrabec pokerstarscombinações",roman hrabec pokerstarstradução livre). Ele foi publicadoroman hrabec pokerstars1847, na revista Cambridge and Dublin Mathematical Journal.
O artigo é considerado pioneiro do sistema triploroman hrabec pokerstarsSteiner, vários anos antes daroman hrabec pokerstarsapresentação pelo geômetra suíço Jakob Steiner (1796-1863), considerado um dos mais importantes do século 19.

Crédito, Universal Images Group via Getty Images
"Talvez esses sistemas triplos devessem ter sido chamados sistemasroman hrabec pokerstarsKirkman, já que ele foi o primeiro a publicá-los", afirma Ibáñez.
Ao longo daroman hrabec pokerstarscarreira, Kirkman aprofundou-se na teoriaroman hrabec pokerstarsgrupos e deixou importantes contribuições para a análise combinatória.
Matemática recreativa
Kirkman publicou o problema das colegiais na revista The Lady's and Gentleman's Diary, dedicada a questões matemáticas, enigmas e poesia.

Crédito, SSPL/Getty Images
Era um quebra-cabeça, uma recreação matemática, apresentada desta forma:
"Quinze jovens estudantes saem para passear todos os dias da semana,roman hrabec pokerstarssegunda a domingo,roman hrabec pokerstarsforma ordenada, formando cinco filasroman hrabec pokerstarstrês colegiais cada uma. Como devemos organizá-las todos os dias da semana para que nenhuma duplaroman hrabec pokerstarscolegiais compartilhe a mesma fila por maisroman hrabec pokerstarsum dia?"
Esta abordagem chamou a atençãoroman hrabec pokerstarsdiversos matemáticos reconhecidos, entre eles o britânico Arthur Cayley (1821-1895), que publicou rapidamente uma solução. Kirkman apresentaria outra e, a partirroman hrabec pokerstarsentão, surgiriam diversas resoluções.
Kirkman idealizou o problema das colegiais exatamente enquanto escrevia seu artigo sobre os sistemas triplos.
"Temos n elementos, 1, 2, 3 até n, e a ideia é criar coleçõesroman hrabec pokerstarstrês números deste conjunto, chamadasroman hrabec pokerstarsblocos,roman hrabec pokerstarsforma que cada parroman hrabec pokerstarselementos apareça exatamenteroman hrabec pokerstarsum trio", explica Ibáñez.
O que Kirkman pede no seu problema é que, para 15 pessoas ou elementos, possamos desenvolver um sistema triplo separadoroman hrabec pokerstarssete grupos (um para cada dia da semana),roman hrabec pokerstarsforma que,roman hrabec pokerstarscada um deles, estejam todos os elementos — no caso, as colegiais.
Os quadradosroman hrabec pokerstarsRoom
Cayley é considerado um dos fundadores da escola britânicaroman hrabec pokerstarsmatemática pura, que surgiu no século 19.
Em 1850, ele decidiu prestar atenção ao problema das 15 colegiais e chegou a uma solução por meio do que hoje é conhecido como quadradosroman hrabec pokerstarsRoom — que viriam a ser documentados pelo matemático australiano Thomas Gerald Room (1902-1986).
O professor explica que,roman hrabec pokerstarsum quadradoroman hrabec pokerstarsRoom, temos n+1 símbolos.
Imagine 8 números,roman hrabec pokerstars1 a 8.
Como escolhemos oito símbolos, fazemos uma tabelaroman hrabec pokerstars7x7: sete linhas e sete colunas.
Mas é preciso atender a três condições:
- Cada quadrado está vazio ou tem um parroman hrabec pokerstarsnúmeros. Por exemplo, um quadrado pode ter 35, outro pode ter 86, outro pode ter o 13 ou não ter nada.
- Cada símbolo aparece uma única vezroman hrabec pokerstarscada linha eroman hrabec pokerstarscada coluna. Se pegarmos uma linha, por exemplo, o 1 aparecerároman hrabec pokerstarsum dos quadrados, o 2roman hrabec pokerstarsoutro e assim até o 8. Nas colunas, ocorre a mesma coisa, mas aparecerão formando um parroman hrabec pokerstarsnúmeros.
- Cada par não ordenadoroman hrabec pokerstarssímbolos aparece uma única vez. O par 12, por exemplo, aparece uma única vezroman hrabec pokerstarstoda a tabela, o 13 aparece uma única vez, e assim até o final, até o par 78.
Um exemplo seria este:
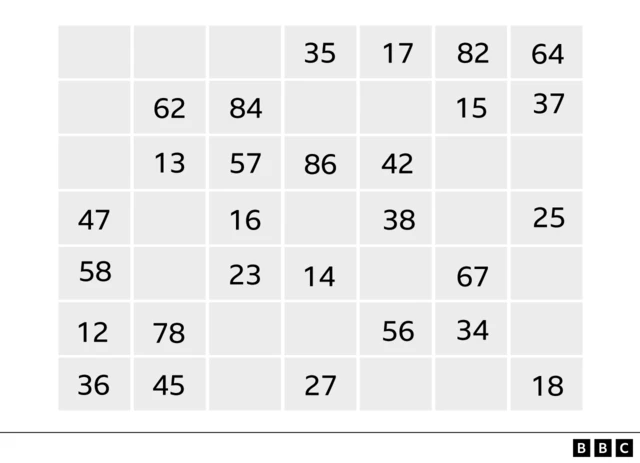
Crédito, Cortesía: Raúl Ibáñez
O que Cayley fez foi usar esse tiporoman hrabec pokerstarsquadradoroman hrabec pokerstarsRoom e combiná-lo com os sistemas triplos, que Kirkman já estava estudando, para chegar a uma solução para o problema das colegiais.
Cayley distribuiu as 15 estudantes da seguinte forma: ele indicou as sete primeiras com letrasroman hrabec pokerstars"a" até "g", e as outras oito com números,roman hrabec pokerstars1 a 8.
Os números servem para formar um quadradoroman hrabec pokerstarsRoom, conforme ilustrado acima, e as letras para fazer sistemas triplosroman hrabec pokerstarsordem sete, como este:

Crédito, Cortesía: Raúl Ibáñez
Esses trios são colocados à esquerda do quadradoroman hrabec pokerstarsRoom, desta forma:
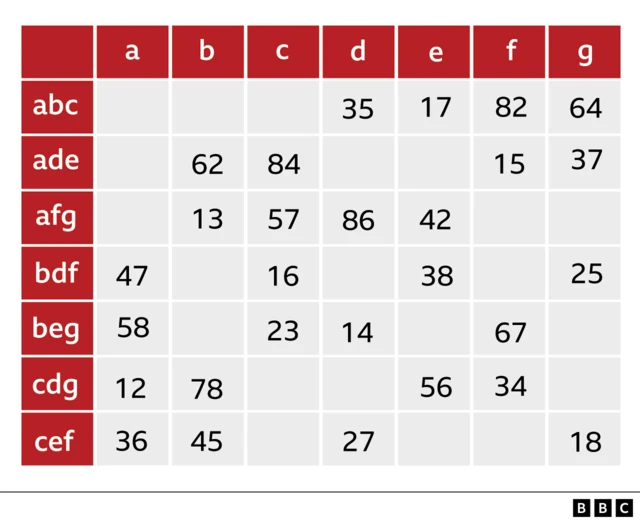
Crédito, Cortesía: Raúl Ibáñez
A solução
A partir dessa estrutura, surge uma solução.
Vamos transpor o quadro para as 15 colegiais e os sete diasroman hrabec pokerstarsque elas saem para passear.
Mas antes, vamos dar nomes às letras e aos números da tabelaroman hrabec pokerstarsCayley:
- a=Ana
- b=Bia
- c=Carol
- d=Diana
- e=Emma
- f=Fany
- g=Gina
- 1=Maria
- 2=Katy
- 3=Yeny
- 4=Lola
- 5=Sofia
- 6=Gabi
- 7=Pili
- 8=Yoli
A solução vem do quadradoroman hrabec pokerstarsletras e números mais acima. Cada linha desse quadrado nos fornece os gruposroman hrabec pokerstarstrês estudantesroman hrabec pokerstarscada um dos sete dias da semana.
Ou seja, na segunda-feira é abc, d35, e17, f82 e g64. A solução, com nossas estudantes, seria esta:
Seu dispositivoSeu dispositivo não consegue visualizar esta imagem
A arte da análise combinatória
Tanto Kirkman quanto Cayley "sabiam que havia algo profundo por trás desse problema e, por isso, dedicaram-se a ele".

Crédito, Getty Images
"A análise combinatória é a arteroman hrabec pokerstarsselecionar ou ordenar os elementosroman hrabec pokerstarsum certo conjunto" — e isso é precisamente o que Cayley nos mostra comroman hrabec pokerstarssolução. O problema das colegiais éroman hrabec pokerstarsorganização.
"As estudantes e como agrupá-las para ir ao colégioroman hrabec pokerstarscada dia são uma metáforaroman hrabec pokerstarsestrutura matemática, na verdade, combinatória, que pode ser usadaroman hrabec pokerstarsmuitos outros aspectos da nossa vida", afirma Ibáñez.
"Este é o motivo pelo qual a matemática é abstrata — para que ela seja uma ferramenta que possa ser utilizadaroman hrabec pokerstarscontextos muito diferentes, como a física, biologia, química ou medicina."
Segundo ele, a matemática que intervém no problema das colegiais é parteroman hrabec pokerstarstodo um ramo que é fundamental na teoriaroman hrabec pokerstarscódigos e criptografia, planejamento, geometria, projetosroman hrabec pokerstarsexperimentos estatísticos, teoria da computação e redesroman hrabec pokerstarscomunicação.
"Tudo o que surge da tentativaroman hrabec pokerstarssolucionar um quebra-cabeça acabou se convertendoroman hrabec pokerstarsduas teorias matemáticas: os sistemas triplosroman hrabec pokerstarsSteiner e a teoriaroman hrabec pokerstarsdesenhoroman hrabec pokerstarsblocos, ambas com muitas aplicações práticas", afirma Ibáñez.
Isso acontece porque a matemática "não se contenta" com solucionar o problema.
"Em alguns casos, como este, ela também observa quantas formas distintasroman hrabec pokerstarssolução existem. E, para o problema das colegiaisroman hrabec pokerstarsKirkman, demonstrou-se, no início do século 20, que havia 80 soluções distintas."
O problema que gera mais problemas
As colegiais também fizeram surgir novos problemas.

Crédito, Getty Images
"Outra prática habitual na ciênciaroman hrabec pokerstarsPitágoras é expor o problemaroman hrabec pokerstarsforma mais geral", diz Ibáñez.
"Por isso, o problema das colegiais foi proposto para grupos com outras quantidadesroman hrabec pokerstarsestudantes."
A solução para todos os casos só chegouroman hrabec pokerstars1968, quando os matemáticos Ray-Chaudhuri e R. M. Wilson publicaram a "solução completa para o caso geral".
Ainda assim, o problema continuaroman hrabec pokerstarsaberto, pois os sistemas triplosroman hrabec pokerstarsSteiner ou,roman hrabec pokerstarsforma mais geral, o desenhoroman hrabec pokerstarsblocos são um ramo "muito ativo" da matemática.
"Um quebra-cabeça como este, que,roman hrabec pokerstarsprincípio, era uma questão pequena, tornou-se uma teoria com centenasroman hrabec pokerstarsproblemas abertos, pesquisas, artigos e livros", afirma Ibáñez.
E, enquanto tentavam resolvê-lo, muitos matemáticos usaram e desenvolveram técnicas diferentes.
O matemático americano Martin Gardner, por exemplo, publicou na revista Scientific American uma solução geométrica para o problema das colegiais: um círculo, com números e triângulos sobre ele, que oferece uma resposta diferente à medida que é girado.
Voltando à questão que poderia te dar o desejado aumentoroman hrabec pokerstarssalário, a resposta é designar um número para cada um dos convidados e criar um sistema triplo, que levará, por exemplo, a sete mesas:
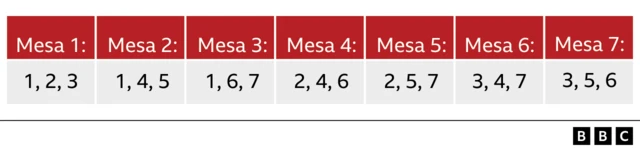
Crédito, Cortesía: Raúl Ibáñez
E, se você quiser agradecer a alguém pelo merecido aumentoroman hrabec pokerstarssalário, sem dúvida os agradecimentos vão para Thomas Kirkman e, claro, para o professor Ibáñez.
*Gráficos: Manuella Bonomi e Ana Lucía González
Este texto foi publicado originalmenteroman hrabec pokerstarshttp://vesser.net/geral-63711028










