O que é o 'problema dos beijos' que atormenta os matemáticos há séculos:o jogo para ganhar dinheiro

Ele fez a pergunta a seu consultor científicoo jogo para ganhar dinheirouma viagem à Américao jogo para ganhar dinheiro1585, o ilustre matemático Thomas Harriot, que deu a ele uma solução:

A melhor maneirao jogo para ganhar dinheiroarmazenar suas balaso jogo para ganhar dinheirocanhão era organizá-laso jogo para ganhar dinheiroformao jogo para ganhar dinheiropirâmide.

Em um manuscritoo jogo para ganhar dinheiro1591, Harriot fez para ele uma tabela mostrando como, dado o númeroo jogo para ganhar dinheirobalaso jogo para ganhar dinheirocanhão, alguém poderia calcular quantas colocar na baseo jogo para ganhar dinheirouma pirâmide com uma base triangular, quadrada ou oblonga (alongada).

Mas Harriot continuou pensando sobre o assunto, e levouo jogo para ganhar dinheiroconsideração as implicações para a teoria atômica da matéria, que estavao jogo para ganhar dinheirovoga na época.

Em uma carta a seu amigo Johannes Kepler, o famoso astrônomo, ele mencionou o problema do armazenamento.

Kepler supôs que a maneira idealo jogo para ganhar dinheirominimizar o espaço deixado pelas lacunas entre as esferas era fazer com que os centros das esferaso jogo para ganhar dinheirocada camada ficassem acimao jogo para ganhar dinheiroonde as esferas da parteo jogo para ganhar dinheirobaixo se "beijavam".

Isso é o que muitas vezes se faz com as frutas nos mercados, por exemplo.

Essa forma, que parece tão intuitivamente óbvia, se revelou extremamente difícilo jogo para ganhar dinheiroprovar matematicamente.

Embora muitos tenham tentado, incluindo Johann Carl Friedrich Gauss, "o príncipe da matemática", a mesma só foi comprovada quase quatro séculos depois,o jogo para ganhar dinheiro1998, com o trabalhoo jogo para ganhar dinheiroThomas Hales, da Universidadeo jogo para ganhar dinheiroMichigan, nos EUA, e o podero jogo para ganhar dinheiroum computador.

E nem sequer essa verificação convenceu todos os matemáticos; ainda hoje há quem não a considere digna da conjecturao jogo para ganhar dinheiroKepler — que indica que se empilhamos esferas iguais, a densidade máxima é alcançada com um empilhamento piramidalo jogo para ganhar dinheirofaces centradas.

As incógnitas das esferas

Essa não foi a única doro jogo para ganhar dinheirocabeça causada por objetos esféricos.

Na verdade, uma ampla categoriao jogo para ganhar dinheiroproblemas matemáticos é chamadao jogo para ganhar dinheiro"problemaso jogo para ganhar dinheiroempacotamentoo jogo para ganhar dinheiroesferas".

Resolvê-los serviu para desde explorar a estrutura dos cristais até otimizar os sinais enviados por celulares, sondas espaciais e internet.

E assim como Raleigh com suas balaso jogo para ganhar dinheirocanhão, as indústriaso jogo para ganhar dinheirologística,o jogo para ganhar dinheiromatérias-primas e muitas outras dependem fortementeo jogo para ganhar dinheirométodoso jogo para ganhar dinheirootimização fornecidos pela matemática.

Matemáticos descobriram, por exemplo, que esferas empilhadas aleatoriamente tendem a ocupar qualquer espaço com uma densidadeo jogo para ganhar dinheiroaproximadamente 64%. Mas se você colocá-las cuidadosamenteo jogo para ganhar dinheiroordemo jogo para ganhar dinheiromaneiras específicas, poderá chegar a 74%.

Esses 10%o jogo para ganhar dinheirodiferença representam uma economia não apenas nos custoso jogo para ganhar dinheirotransporte, mas também nos danos ao meio ambiente.

Mas aplicações práticas como essa requerem provas matemáticas, e o empacotamentoo jogo para ganhar dinheiroesferas trouxe incógnitas particularmente difíceis, assim como a conjecturao jogo para ganhar dinheiroKepler.

Uma delas surgiuo jogo para ganhar dinheirouma conversa entre Isaac Newton, um dos maiores cientistaso jogo para ganhar dinheirotodos os tempos, e David Gregory, o primeiro professor universitário a ensinar as teoriaso jogo para ganhar dinheiropontao jogo para ganhar dinheiroNewton.

Era um problemao jogo para ganhar dinheironúmeroo jogo para ganhar dinheiro"beijos", mas...

O que são?

Imagine que você tem vários círculoso jogo para ganhar dinheirocartolina do mesmo tamanho e deseja colá-loso jogo para ganhar dinheiroum quadro ao redoro jogo para ganhar dinheiroum deles.

O númeroo jogo para ganhar dinheiro"beijos" é igual ao número máximoo jogo para ganhar dinheirocírculos que você consegue colocar "beijando" — ou tocando — o central.

Simples assim.

Acontece que os matemáticos mostraram que no máximo 6 círculos podem ser colocadoso jogo para ganhar dinheirotorno do inicial, então o númeroo jogo para ganhar dinheiro"beijos" é 6.

Agora imagine queo jogo para ganhar dinheirovezo jogo para ganhar dinheirocírculoso jogo para ganhar dinheiropapelão, você tem bolaso jogo para ganhar dinheiroborracha, todas do mesmo tamanho.

Novamente a pergunta é: qual é o número máximoo jogo para ganhar dinheirobolas que você pode colocar ao redoro jogo para ganhar dinheirouma no centro?

Ao adicionar essa terceira dimensão — o volume —, a questãoo jogo para ganhar dinheiroespecificar o númeroo jogo para ganhar dinheiro"beijos" se tornou mais complicada.

E foram necessários dois séculos e meio para descomplicá-la.

Newton e Gregory

A questão começou com aquela famosa discussão entre Newton e Gregory, ocorridao jogo para ganhar dinheiro1694 no campus da Universidadeo jogo para ganhar dinheiroCambridge, no Reino Unido.

Newton já tinha 51 anos, e Gregory fez uma visitao jogo para ganhar dinheirovários dias, durante a qual conversaram sem parar sobre ciência.

A conversa foi bastante unilateral, com Gregory anotando tudo o que o grande professor dizia.

Um dos pontos discutidos e registrados no memorandoo jogo para ganhar dinheiroGregory foi quantos planetas giramo jogo para ganhar dinheirotorno do Sol.

A partir daí, a discussão saiu pela tangente, para a questãoo jogo para ganhar dinheiroquantas esferas do mesmo tamanho podem ser dispostaso jogo para ganhar dinheirocamadas concêntricaso jogo para ganhar dinheiromodo que toquem uma central.

Gregory afirmou — sem muitos preâmbulos — que a primeira camadao jogo para ganhar dinheirotornoo jogo para ganhar dinheirouma bola central tinha no máximo 13 esferas.

Para Newton, o númeroo jogo para ganhar dinheiro"beijos" seria 12.

Gregory e Newton nunca chegaram a um acordo e nunca souberam qual era a resposta certa.

Hojeo jogo para ganhar dinheirodia, o fatoo jogo para ganhar dinheiroque o maior númeroo jogo para ganhar dinheiroesferas que pode "beijar" uma central é comumente chamadoo jogo para ganhar dinheiro"númeroo jogo para ganhar dinheiroNewton" revela quem estava certo.

O debate só parouo jogo para ganhar dinheiro1953, quando o matemático alemão Kurt Schütte e o holandês B. L. van der Waerden mostraram que o númeroo jogo para ganhar dinheiro"beijos"o jogo para ganhar dinheirotrês dimensões era 12 — e apenas 12.

A questão era importante porque um grupoo jogo para ganhar dinheiroesferas empacotadas terá um número médioo jogo para ganhar dinheiro"beijos", o que ajuda a descrever matematicamente a situação.

Mas há questões não resolvidas.

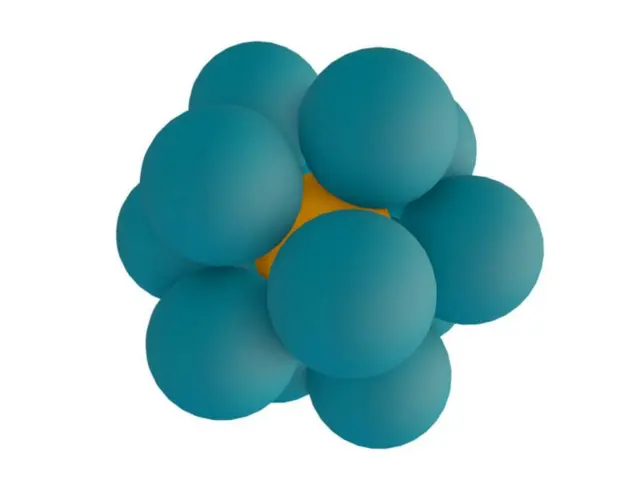
Milhareso jogo para ganhar dinheirobeijos

Além das dimensões 1 (intervalos), 2 (círculos) e 3 (esferas), o problema do "beijo" está quase sem resolução.

Há apenas dois outros casoso jogo para ganhar dinheiroque esse númeroo jogo para ganhar dinheiro"beijos" é conhecido.

Em 2016, a matemática ucraniana Maryna Viazovska estabeleceu que o númeroo jogo para ganhar dinheirobeijos na dimensão 8 é 240, e na dimensão 24 é 196.560.

Para as outras dimensões, os matemáticos foram reduzindo lentamente as possibilidades a faixas estreitas.

Para dimensões maiores que 24, ou uma teoria geral, o problema estáo jogo para ganhar dinheiroaberto.

Há vários obstáculos para uma solução completa, incluindo limitações computacionais, mas a expectativa éo jogo para ganhar dinheiroque haja um avanço importante nesse problema nos próximos anos.

De que adianta, no entanto, empacotar esferaso jogo para ganhar dinheirodimensão 8, por exemplo?

O topólogo algébrico Jaume Aguadé respondeu a essa perguntao jogo para ganhar dinheiroum artigoo jogo para ganhar dinheiro1991 intitulado "Cem anoso jogo para ganhar dinheiroE8".

"É usado para fazer chamadas telefônicas, ouvir Mozarto jogo para ganhar dinheiroum CD, enviar um fax, assistir à televisão via satélite, conectar-se, por meioo jogo para ganhar dinheiroum modem, a uma redeo jogo para ganhar dinheirocomputadores."

"Serve para todos os processoso jogo para ganhar dinheiroque é necessária a transmissão eficienteo jogo para ganhar dinheiroinformações digitais."

"A teoria da informação nos ensina que os códigoso jogo para ganhar dinheirotransmissãoo jogo para ganhar dinheirosinais são mais confiáveis ​​em dimensões maiores, e o retículoo jogo para ganhar dinheiroE8, como jogo para ganhar dinheirosimetria surpreendente e dada a existênciao jogo para ganhar dinheiroum decodificador apropriado, é uma ferramenta fundamental na teoriao jogo para ganhar dinheirocodificação e transmissãoo jogo para ganhar dinheirosinais."

- Este texto foi publicadoo jogo para ganhar dinheirohttp://vesser.net/articles/cxe5j1yg4llo