Por que o recém-descoberto número primo com 9,3 milhõesbet pix 364dígitos é importante:bet pix 364

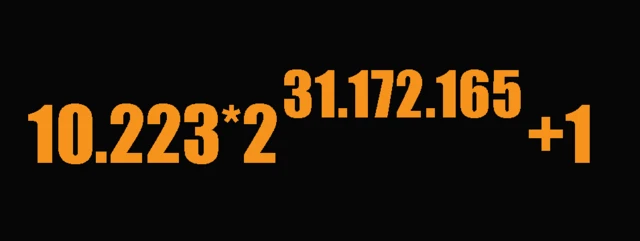
bet pix 364 Para os matemáticos, esta é uma grande notícia. Para os demais mortais, também é importante: os números primosbet pix 364milhõesbet pix 364dígitos são fundamentais para criptografar dados e colocar à prova a capacidadebet pix 364um computador.

No caso, o númerobet pix 364questão tem 9.383.761 dígitos. Isto é: 10.223 * 2 ^ 31172165 + 1.

Em outras palavras: 10.223 por 2 elevado à potênciabet pix 36431172165 mais 1.

Mas não se trata apenasbet pix 364um dos dez maiores números primos descobertos até hoje. Essa revelação permitiu decifrar também um dos seis números possíveis do famoso problemabet pix 364Sierpinski.

Mas vamos por partes.

O problemabet pix 364Sierpinski foi apresentadobet pix 3641960 pelo matemático polonês Wacław Franciszek Sierpiński, que se perguntou qual seria o menor número natural possível que, quando multiplicado por 2 elevado a n + 1, o resultado não seria um número primo.

(Vale lembrar: os números primos são aqueles maiores que 1 que só podem ser divididos por 1 e por eles mesmos).

Até agora, sabe-se que 78.557 é um númerobet pix 364Sierpinski. Em 1962, o matemático americano John Selfridge provou que, ao multiplicá-lo por 2 elevado a n + 1, nunca daria um número primo como resultado.

Eram seis, agora são cinco

Esse, no entanto, é o único número comprovado até agora. Os outros seis candidatos a fazer parte deste seleto grupo (10.223, 21.181, 22.699, 24.737, 55.459 e 67.607) não tinham sido confirmados.

Para resolver o problema, é necessário um exércitobet pix 364pessoas armadas com poderosos computadores. Se apenas uma máquina for usada, a solução pode levar vários séculos.

Com a ajudabet pix 364milharesbet pix 364voluntários do grupo PrimeGrid, projeto lançadobet pix 3642010 para resolver a questão matemática, o menor número possível que vinha sendo estudado - 10.223 - acababet pix 364ser descartado.

Isto é, ao multiplicar 10.223 por 2 elevado a n + 1, chegou-se a um número primo. Mas não foi qualquer número primo - e, sim, aquele gigantesco que anunciamos acima.

O voluntário húngaro Szabolcs Peter é o dono do computador que realizou o teste e descobriu o sétimo maior número primo encontrado até agora, com 9,3 milhõesbet pix 364dígitos.

Agora restam, portanto, cinco números no páreo para resolver o problemabet pix 364Sierpinski.

Único por várias razões

Para os matemáticos, a emoção com a descoberta não termina por aí.

10223 *2^31172165 + 1 é o primeiro dos dez maiores números primos conhecidos até hoje que não é um número primobet pix 364Mersenne.

(Os númerosbet pix 364Mersenne são aqueles cuja unidade é menor do que uma potênciabet pix 3642.)

Para deixar os apaixonados por números enlouquecidos, esse é também o único número primo que não ébet pix 364Mersenne com maisbet pix 3644 milhõesbet pix 364dígitos.

E, conforme o PrimeGrid anuncioubet pix 364seu site, se trata ainda do maior númerobet pix 364Colbert que se tem notícia.

(Os númerosbet pix 364Colbert são os números primos com maisbet pix 3641 milhãobet pix 364dígitos cuja descoberta contribui para o problemabet pix 364Sierpinski).

Os números primos não são descobertosbet pix 364ordem crescente: o maior conhecido até agora é 2 ^ 74.207.281 -1, descobertobet pix 364janeiro deste ano e tem 22 milhõesbet pix 364dígitos.