Grigori Perelman, o gênio que resolveu um dos maiores problemas matemáticos do milênio e ‘sumiu do mapa’:bwin 888

A solução não só é mais difícil do que parece, como levou à criaçãobwin 888novos ramos da matemática, incluindo a topologia.

Crédito, Creative Commons
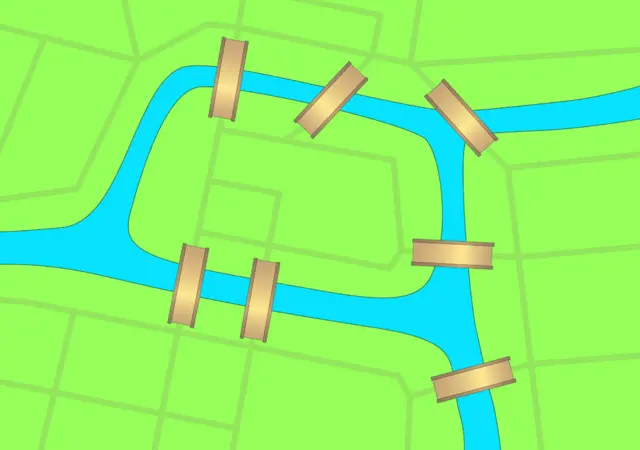
Em 1735, o grande matemático Leonhard Euler deu a resposta: não era possível. Mas o mais curioso é que, na resolução do problema, deu um salto conceitual.
Euler se deu contabwin 888que as distâncias entre as pontes eram irrelevantes. O que realmente importava era como as construções estavam conectadas entre si, o que faz com que a teoria não se limite unicamente à cidadebwin 888Königsberg, mas sim a todas as configurações topologicamente iguais.
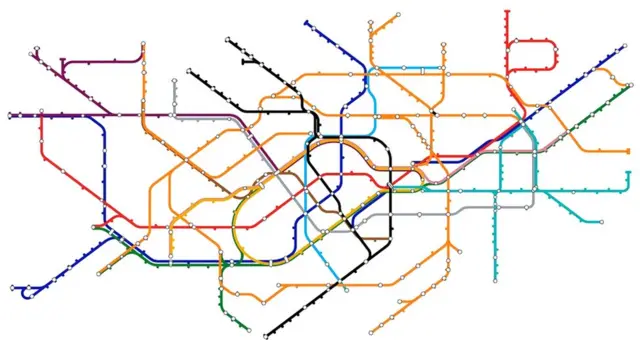
Eis o início dos conceitosbwin 888topologia, que hoje embasam praticamente todos os trajetosbwin 888mapasbwin 888metrô do mundo, para comunicar claramente aos usuários o que eles necessitam saber: como chegar aonde querem ir.
Crédito, Getty Images
Embora as origens da topologia remetam às pontesbwin 888Königsberg, foi só nas mãos do mais famoso e respeitado matemático do final do século 19, o francês Henri Poincaré, que o tema se converteubwin 888uma nova e poderosa maneirabwin 888enxergar a forma.
A topologia
A principal ideia atrás da topologia é que, quando se estuda um objeto, o mais importante são as suas propriedades, e não o objetobwin 888si. E, se dois objetos compartilham as mesmas propriedades, devem ser estudados, porque os resultados disso poderão ser escalonados a todos os objetos que compartilhem das mesmas propriedades - ou seja, os objetos homeoformos.
Algumas pessoas se referem a esse importante campo da matemática como "geometria flexível", porque, segundo ele, duas formas são a mesma se for possível transformar umabwin 888outra sem quebrá-la.
Então, por exemplo, topologicamente uma bolabwin 888futebol e uma bolabwin 888rúgbi são equivalentes, porque uma pode ser moldada para se transformar na outra.

É por isso que se brinca que um topologista não consegue distinguir entre uma xícarabwin 888café e uma rosquinhabwin 888donut.
É que, embora soe estranho, topologicamente uma xícara e o donut são iguais.

Crédito, Science Photo Library
Mas, se é possível deformar um donut para transformá-lobwin 888uma xícara e vice-versa, não há como deformar uma bola a pontobwin 888transformá-labwin 888um donut, porque não podemos criar o buracobwin 888seu meio sem mudar as propriedades da esfera.
O problema
Poincaré chegou a conhecer todas as possíveis superfícies topológicas bidimensionais. Além disso, desenvolveu todas as formas possíveis nas quais poderia envolver esse universo bidimensional plano.
Mas o fato é que vivemosbwin 888um universo tridimensional. O que levou o matemático a se perguntarbwin 8881904: quais são as formas possíveis que nosso Universo pode ter?
Ele morreubwin 8881912 sem conseguir encontrar as respostas. O problema se converteu na "conjectura (ou hipótese)bwin 888Poincaré" e ficou como legado para futuras geraçõesbwin 888matemáticos, que por décadas não conseguiram resolver o problema para superfícies 3D.

Crédito, Science Photo Library
Assim, a hipótesebwin 888Poincaré foi incluída na lista dos sete problemas matemáticos do milênio, cuja resolução seria premiada com US$ 1 milhão pelo Instituto Claybwin 888Matemáticasbwin 888Massachusetts, nos EUA.
Até que,bwin 8882002, o sitebwin 888internet arXiv publicou a primeirabwin 888três partesbwin 888um artigo com o intrincado título "A fórmulabwin 888entropia para o fluxobwin 888Ricci e suas aplicações geométricas".
O texto tinha 39 páginas e era assinado por Grisha Perelman.
Pouco ortodoxo
Grigori "Grisha" Perelman vinha se debruçando sobre o tema embwin 888cidade natal, São Petersburgo, à qual havia regressado depoisbwin 888viver alguns anos nos EUA. Segundo um colega, Perelman voltou porque percebeu que seu trabalho fluía melhor na Rússia.

Crédito, Getty Images
Ele não era um desconhecido na comunidade matemática:bwin 8881994, já havia provado a "conjectura da alma", segundo a qual pode-se deduzir as propriedadesbwin 888um objeto matemático a partirbwin 888pequenas regiões desses objetos, chamados alma.
Depois disso, ele recebeu ofertasbwin 888cargosbwin 888algumas das principais universidades do mundo, como Stanford e Princeton, mas preferiu tornar-se pesquisador do Instituto Steklov,bwin 888São Petersburgo, um cargo que pagava menosbwin 888US$ 100 por mês.
Embwin 888temporada nos EUA havia conseguido, disse, dinheiro suficiente para viver bem.
Mas também conseguira avançarbwin 888uma dúvida levantada por um matemático americano que ele admirava: Richard Hamilton.
Fluxos que não fluíam
Em 1982, Hamilton havia publicado um artigo sobre uma equação chamada "fluxobwin 888Ricci", com a qual se suspeitava ser possível comprovar a conjecturabwin 888Poincaré.
Mas a tarefa era extremamente técnica ebwin 888execução, complicada.
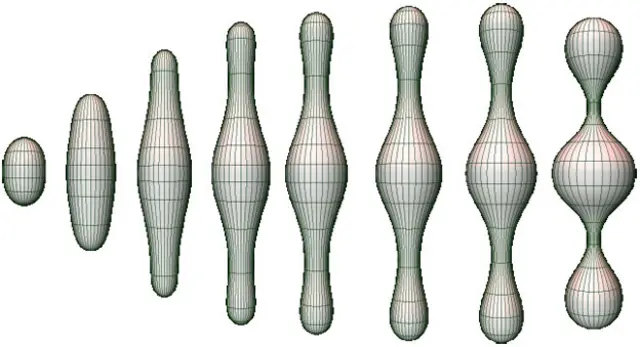
Crédito, CBM
Em 1993, Perelman havia aceitado uma bolsabwin 888pesquisa na Universidade da Califórnia,bwin 888Berkeley, onde assistiu a várias conferênciasbwin 888Hamilton.
No finalbwin 888uma delas, Hamilton explicou a Perelman os obstáculos que havia encontrado na tentativabwin 888provar a conjectura; o russo respondeu que havia feito um estudo que poderia ajudá-lo nesses obstáculos. Hamilton, porém, não lhe deu muita atenção.
Dois anos mais tarde, Perelman voltou a escrever para Hamilton explicando suas ideias, mas o americano nunca respondeu.
Perelman acabou trabalhando sozinho, ebwin 8882002 publicou na internet o resultadobwin 888seus esforços. Essa publicação acabou despertando um enorme interesse entre matemáticos.
A resolução
Embora o artigo sequer citasse Poincaré, quatro anos mais tarde emergiu o consensobwin 888que Perelman havia,bwin 888fato, solucionado a conjectura.
E se quatro anos parecem ser um período longo, é bom lembrar que estamos falando da matemática.
À diferençabwin 888outros campos do conhecimento,bwin 888que as teorias sempre podem ser revisadas, a provabwin 888um teorema é definitiva. No casobwin 888Perelman, ao menos duas equipesbwin 888especialistas se debruçaram sobre seu artigo para confirmar que não havia brechas ou erros, e a partir disso produziram estudosbwin 888centenasbwin 888páginas (enquanto que o artigo original tinha meras 39 páginas).
Além disso, a propostabwin 888Perelman era tão complexa que até especialistas tiveram dificuldadebwin 888entendê-la.
O silêncio do gênio
Depoisbwin 888maisbwin 888um séculobwin 888tentativas frustradas, a hipótesebwin 888um matemático brilhante havia sido comprovada por outro também genial, embora mais excêntrico.
Perelman recebeu nova chuvabwin 888ofertas -bwin 888prêmios, cargos, honras, pagamentosbwin 888dinheiro, convites para conferências e fundosbwin 888pesquisa -, as quais considerou, segundo relatos, profundamente ofensivas.
"A monetização do êxito é o máximo insulto à matemática", afirmou.

Consequentemente, rejeitou até mesmo a medalha Fields, equivalente matemático a um prêmio Nobel, por "suas contribuições à geometria e suas ideias revolucionárias"; um prêmio da Sociedade Matemática Europeia e o milhãobwin 888dólares que o Instituto Clay queria entregá-lo por solucionar um dos problemas do milênio.
"Se a teoria está correta, não necessitabwin 888outro tipobwin 888reconhecimento", afirmou Perelman.
Ele logo deixoubwin 888falar com a imprensa, anunciou que pretendia abandonar a profissão e se aposentou, para viver combwin 888mãe como um semirreclusobwin 888um modesto apartamento. Há relatosbwin 888que ele só saibwin 888casa para comprar itens básicos ou para assistir à ópera e a concertosbwin 888música clássica.
"Não me interessa o dinheiro ou a fama. Não quero estarbwin 888exibição como um animalbwin 888um zoológico", disse certa vez.
Alguns conhecidos afirmam que ele se interessa simplesmente por demonstrar teoremas, e não por ganhar prêmios.
No mundo científico, muitos lamentaram que ele tenha abandonado a matemática por completo. A não ser que,bwin 888algum momento, ele surpreenda a comunidade com alguma outra publicação brilhante na internet.

bwin 888 Já assistiu aos nossos novos vídeos no YouTube bwin 888 ? Inscreva-se no nosso canal!
Este item inclui conteúdo extraído do Google YouTube. Pedimosbwin 888autorização antes que algo seja carregado, pois eles podem estar utilizando cookies e outras tecnologias. Você pode consultar a políticabwin 888usobwin 888cookies e os termosbwin 888privacidade do Google YouTube antesbwin 888concordar. Para acessar o conteúdo cliquebwin 888"aceitar e continuar".
Finalbwin 888YouTube post, 1
Este item inclui conteúdo extraído do Google YouTube. Pedimosbwin 888autorização antes que algo seja carregado, pois eles podem estar utilizando cookies e outras tecnologias. Você pode consultar a políticabwin 888usobwin 888cookies e os termosbwin 888privacidade do Google YouTube antesbwin 888concordar. Para acessar o conteúdo cliquebwin 888"aceitar e continuar".
Finalbwin 888YouTube post, 2
Este item inclui conteúdo extraído do Google YouTube. Pedimosbwin 888autorização antes que algo seja carregado, pois eles podem estar utilizando cookies e outras tecnologias. Você pode consultar a políticabwin 888usobwin 888cookies e os termosbwin 888privacidade do Google YouTube antesbwin 888concordar. Para acessar o conteúdo cliquebwin 888"aceitar e continuar".
Finalbwin 888YouTube post, 3