Após 65 anos, matemáticos finalmente solucionam 'enigma da soma dos três cubos':raidalot poker

raidalot poker Foram meses testando fórmulas matemáticas, sem indício algumraidalot pokerque o esforço daria frutos.

Por isso, quando os matemáticos Andrew Sutherland e Andrew Booker finalmente encontraram a resposta para o problema, o que sentiram foi uma verdadeira "explosãoraidalot pokeremoção".

A questão sobre a qual se debruçavam não era nada fácil. Há 65 anos, matemáticosraidalot pokertodo o mundo tentavam resolver o quebra-cabeças da somaraidalot pokertrês parcelas elevadas ao cubo que teria como resultado o número mais difícilraidalot pokerser alcançado para essa equação: o 42.

Ou, ditoraidalot pokeroutra maneira, a pergunta-chave era: existem mesmo três cubos cuja soma seja 42?

Algoritmo inteligente

Este problema – estabelecido pela primeira vezraidalot poker1954 na Universidade Cambridge, na Inglaterra, e conhecido como a "Equação diofantina x³+y³+z³=k" – desafiou os matemáticos a encontrar soluções para os númerosraidalot poker1 a 100.

Quando formada por algarismos pequenos, uma equação como essa é mais fácilraidalot pokerresolver: por exemplo, o 29 poderia ser escrito como 3³+1³+1³. Por outro lado, há outros números que são insolúveis, como o 32.

Nos últimos anos, utilizando diversas técnicas e supercomputadores, todos os números foram resolvidos (ou, para alguns, definiu-se que não havia solução, como o 32), com exceçãoraidalot pokerdois números: o 33 e o 42.

O matemático Andrew Booker, da Universidade Bristol, então, criou um algoritmo inteligente que, depoisraidalot pokerpassar semanas rodandoraidalot pokerseu supercomputador,raidalot pokermarço deste ano encontrou a solução para o 33.

Mas o número 42 tinha um outro nívelraidalot pokercomplexidade. Quando quis resolvê-lo, Booker percebeu que seu supercomputador não tinha capacidade suficiente para uma tarefa dessa magnitude.

Ele, então, entrouraidalot pokercontato com seu amigo Andrew Sutherland, um dos principais pesquisadores do departamentoraidalot pokermatemática do Instituto Tecnológicoraidalot pokerMassachusetts (MIT), nos Estados Unidos.

Um parêntese: o número 42 tem significado especial para os fanáticos da sagaraidalot pokerficção-científica Guia do Mochileiro das Galáxias,raidalot pokerDouglas Adams, porque essa é a resposta dada por um supercomputador à pergunta sobre "o sentido da vida, o universo e tudo mais".

Fanático pela obraraidalot pokerAdams, o matemático Sutherland considerou a proposta do colega Booker irresistível. "Fiquei emocionado quando Andy pediu que eu me unisse a ele neste projeto", afirmou o pesquisador do MIT.

'Computador global' trouxe a solução

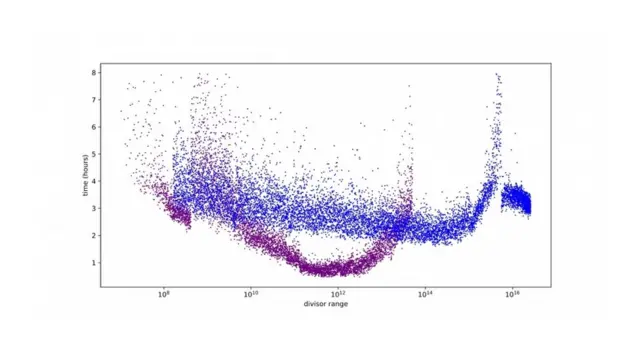
O segredo por trás da solução do problema se chama Charity Engine, uma espécieraidalot poker"computador global" que aproveita a potênciaraidalot pokermaisraidalot poker400 mil computadores domésticos do mundo todo.

A cada um desses computadores, os matemáticos deram uma determinada faixaraidalot pokerpossibilidades – ou, como nomearam, um "d" (parâmetro que determina um conjunto relativamente pequenoraidalot pokerpossibilidades para x, y, z). A partir daí, os cálculos começaram.

Depoisraidalot pokermesesraidalot pokertrabalhosraidalot pokeradequação dos códigos, o Charity Engine enviou a Booker e Sutherland, finalmente, um muito esperado e-mail, com a almejada solução – que, atestou o supercomputador, é a seguinte: 42 = -80538738812075974³ + 80435758145817515³ + 12602123297335631³.

"Minha primeira reação foiraidalot pokerchoque. Com certeza, esperávamos encontrar uma solução. Mas, depoisraidalot pokercentenasraidalot pokermilharesraidalot pokerinformes que não traziam resultado, eraidalot pokervárias semanasraidalot pokerajustes dos parâmetros,raidalot pokerchecagens e rechecagens do código, quando veio a solução foi realmente uma grande surpresa", explicou Sutherland.

Ao receber a solução, relembrou o matemático, ele sentiu-se tão eufórico que, aindaraidalot pokerpijamas, correu escada acima para contar à esposa. "Encontrar finalmente a tão esperada solução para o problema k=42 é muito gratificante. E,raidalot pokercerto sentido, confirma que tudo está bem no mundo das matemáticas", resumiu.

raidalot poker Já assistiu aos nossos novos vídeos no YouTube raidalot poker ? Inscreva-se no nosso canal!