Os 3 grandes paradoxos que tiram o sonopokerstars com brmatemáticos e filósofos:pokerstars com br

pokerstars com br Esta frase é falsa.

Este é um dos paradoxos mais populares e ilustrativos: se é realmente falsa, o que a frase enuncia é verdadeiro, mas se a falsidade enunciada é real, a frase não pode ser falsa.

Paradoxo vem das palavraspokerstars com brlatim e grego que significam "o contrário da opinião comum" e é,pokerstars com bracordo com o dicionário Houaiss:

1. Proposição ou opinião contrária ao comum;

2. Aparente faltapokerstars com brlógica ou nexo; contradição.

Há vários tipos, mas o que eles geralmente têmpokerstars com brcomum é o fatopokerstars com brconseguirem nos fazer parar e pensar, mesmo por um momento. Como quando se lê a frase "para chegar rápido, nada melhor do que ir devagar".

Outras nos acompanharam por anos, às vezes séculos, e algumas têm impulsionado importantes avançospokerstars com brciência, filosofia e matemática.

Ainda é seu navio?

Mudança e identidade. Sobre isso nos fez refletir o historiador, biógrafo e filósofo grego Plutarco (46 - 120 d.C.) durante quase 2.000 anos com o paradoxopokerstars com brTeseu, o mítico rei fundadorpokerstars com brAtenas, filhopokerstars com brEtra e Eseo, ou, segundo outras lendas,pokerstars com brPoseidon.

"O naviopokerstars com brque Teseu e a juventudepokerstars com brAtenas retornarampokerstars com brCreta tinha trinta remos e foi conservado pelos atenienses até o tempopokerstars com brDemetriopokerstars com brFalero. Suas tábuas antigas foram removidas à medidapokerstars com brque introduziram novas madeiras e mais resistentespokerstars com brseu lugar,pokerstars com brmodo que o navio se tornou um exemplo permanente entre filósofos para discutir a questão lógica das coisas que crescem. Um lado sustenta que o navio permanece o mesmo, e o outro diz que não".

Se o navio fosse preservado pelos atenienses até o tempopokerstars com brDemetriuspokerstars com brPhalerus, isso significaria cercapokerstars com br300 anos.

Com tantas reformas, o navio era o mesmo?

E foi além. Se com a madeira velha construíssem outro barco idêntico, qual dos dois seria o original: aquele com as placas originais ou aquele que foi restaurado?

O movimento não existe

Para ir a qualquer lugar, você deve percorrer primeiro a metade da distância, logo, a metade da distância que falta percorrer, depois, a metade da distância que falta, e assim até o infinito, então você nunca chegará lá.

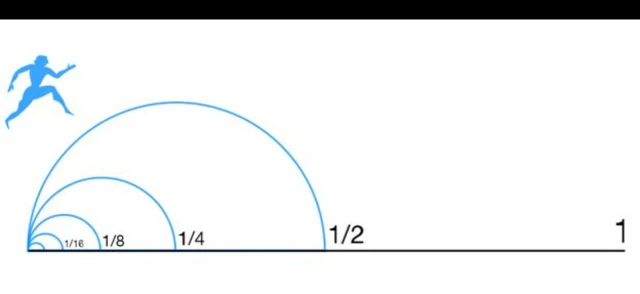
Este é mais um da sériepokerstars com brparadoxos do movimento que o filósofo grego Zenãopokerstars com brElea criou para demonstrar que o Universo é singular e que a mudança, inclusive o movimento, é impossível, como argumentou o seu professor Parmênides.

Se te parecer absurdo, você não está sozinho: foi rejeitado por anos.

No entanto, a matemática ofereceu uma solução formal no século 19 que foi aceitar que 1/2 + 1/4 + 1/8 + 1/16... somam 1.

Embora essa solução teórica atinja determinados propósitos, não respondeu o que estava acontecendo na realidade: como algo pode chegar ao seu destino.

Isso, que entendemos intuitivamente porque o experimentamos diariamente, é mais complexo e, para resolvê-lo, tivemos que esperar até o século 20 para usar teorias que mostrem que a matéria, o tempo e o espaço não são infinitamente divisíveis.

Aquele que fez a matemática cambalear

Agora que já esquentamos os motores, vamos falar sobre um paradoxo que abalou a comunidade matemática no início do século 20, incluindo aquele que o formulou: o filósofo, matemático, lógico e escritor britânico vencedor do Prêmio Nobelpokerstars com brLiteratura Bertrand Russell.

Russell era um dos que estavam impulsionando o logicismo - a tese filosófica que diz que a matemática, ou a maior parte dela, pode ser reduzida à lógica.

Esse projeto incluía empokerstars com brbase a teoriapokerstars com brconjuntospokerstars com brCantor-Frege. Ambos, o alemão Georg Cantor e seu compatriota Gotlob Frege, assumiram que todo predicado definia um conjunto. Assim, o predicado "serpokerstars com brouro" define o conjuntopokerstars com brtodas as coisas que sãopokerstars com brouro.

Soa mais do que óbvio.

Mas Russell descobriu que havia um predicado particular que contradisse a teoria: "não pertence a si mesmo".

Esse é o paradoxopokerstars com brRussell, e é complexo, mas felizmente encontramos uma das explicações mais claras, criada por M. Carmen Márquez García para um cursopokerstars com brSaem Thales - Formação à Distância pela Internet.

Suponhamos que um conhecido especialistapokerstars com brobraspokerstars com brarte decida classificar os quadrospokerstars com brtodo o mundopokerstars com bruma das duas categorias mutuamente excludentes.

Uma categoria,pokerstars com brpoucos quadros, consistepokerstars com brtodas as pinturas que incluem uma imagempokerstars com brsi mesma na cena apresentada na tela. Por exemplo, podemos pintar um quadro, intitulado "Interior",pokerstars com bruma sala e seus móveis - obras penduradas, uma estátua, um pianopokerstars com brcauda - que inclui, pendurado acima do piano, uma pequena pintura da pintura "Interior". Assim, nossa tela incluiria uma imagempokerstars com brsi mesma

A outra categoria, muito mais comum, consistiriapokerstars com brtodos os quadros que não incluem uma imagempokerstars com brsi mesmo. Chamaremos essas obraspokerstars com br"pinturaspokerstars com brRussell". A Mona Lisa, por exemplo, é uma pinturapokerstars com brRussell porque não tem dentro dela mesma uma pequena pintura da Mona Lisa.

Suponhamos também que nosso especialistapokerstars com brarte reúnapokerstars com bruma enorme exposição todas as pinturaspokerstars com brRussell do mundo. Depoispokerstars com brimensos esforços, ele as reúne e as pendurapokerstars com bruma sala enorme.

Orgulhosopokerstars com brsua façanha, o especialista instrui um artista a pintar uma imagem da sala e seu conteúdo.

Quando a pintura ficar pronta, o artista a intitula, com toda propriedade,pokerstars com br"Todas as pinturaspokerstars com brRussell do mundo".

O galerista examina cuidadosamente a pintura e descobre uma pequena falha: na tela, ao lado da pintura da Mona Lisa, há uma representaçãopokerstars com br"Todas as pinturaspokerstars com brRussell do mundo". Isso significa que "Todas as pinturas do mundo" é uma imagem que inclui uma imagempokerstars com brsi mesma e, portanto, não é uma pinturapokerstars com brRussell. Consequentemente, não pertence à exposição e certamente não deve estar pendurado na parede.

O especialista pede ao artista para apagar a pequena representação.

O artista a apaga e retorna para mostrar a imagem ao especialista. Depoispokerstars com brexaminá-la, ele percebe que há um novo problema: a pintura "Todas as pinturaspokerstars com brRussell do mundo" agora não inclui uma imagempokerstars com brsi mesma e, portanto, é uma pinturapokerstars com brRussell, que deveria pertencer à exposição. Consequentemente, deve ser pintado e penduradopokerstars com bralguma parte das paredes, para que o trabalho não inclua todas as pinturaspokerstars com brRussell.

O especialista chama o artista novamente e pede que ele retoque com uma pequena imagem o "Todas as pinturaspokerstars com brRussell do mundo".

Mas uma vez que a imagem foi adicionada, estamos novamente no início da história. A imagem deve ser apagada, posteriormente deve ser pintada e depois excluída, e assim por diante.

Eventualmente, o artista e o especialista perceberão que algo não está funcionando: eles encontraram o paradoxopokerstars com brRussell.

Tendopokerstars com brmente que Russell estava tentando reduzir a matemática para a lógica e o que ele descobriu foi uma brecha nos fundamentos da ciência,pokerstars com brreação não surpreende.

"Eu sentia sobre essas contradições o mesmo que deve sentir um católico fervoroso sobre papas indignos".

Mas não tinha volta: as descobertas não poderiam voltar a ser cobertas novamente.

Embora para alguns matemáticos o assunto era indiferente e não merecia muita reflexão, outros dedicaram a maior parte do seu trabalho intelectual na primeira metade do século 20 a superar o paradoxopokerstars com brRussell... até que se decidiu que um conjunto que contenha a si mesmo realmente não é um conjunto.

A solução não agradou a muitos, nem mesmo a Russell.

M. Carmen Márquez García diz que "a tensão intelectual epokerstars com brconclusão desanimadora cobraram um preço muito caro".

Russell lembraria como depois disto ele "se afastou da lógica matemática com uma espéciepokerstars com brnáusea".

Ele voltou a pensarpokerstars com brsuicídio, mas decidiu não concretizá-lo porque, observou ele, certamente se arrependeria.